ディープラーニングから見えてくる知性の本質を探り
ロボットやAIなど幅広い分野への展開を目指す

情報科学研究科　情報理工学専攻
複合情報工学講座  自律系工学研究室・教授

博士（工学）山本　雅人

プロフィール

1991年北海道大学工学部情報工学科 卒業、1996年同大学院工学研究科システム情報工学専攻 博士後期課程 修了。1996年4月〜1997年7月日本学術振興会特別研究員(PD)。1997年8月より北海道大学大学院工学研究科助手、助教授（准教授）を経て2012年12月に情報科学研究科教授に就任。研究分野は人工生命／人工知能、ソフトコンピューティング、ゲーム情報学、観光情報学。

山本　「生命知能の理解と創造」をテーマに、ディープラーニング（深層学習）などからヒントを得た人工生命や人工知能の研究を行っています。「生命知能」とは脳の部分だけをターゲットにしているのではなく、身体性や関係性も含めた捉え方をしています。ロボットなどの機械には実体があり、実際に動くからこそ出てくる知能があるのではないかというアプローチです。

自律系の研究には大きく３つのジャンルがあり、①人工知能や深層学習などの問題を扱うIntelligence、②人と人、人と機械、あるいは群れといった複数の個体の相互作用や関係性を扱うInteraction、③認知科学や脳計測を含む⼈間の理解を扱うMindの３つです。それぞれの分野で多様な研究を進めていますが、今回はその中で３つのテーマを取り上げたいと思います。

まず一つは「群れ行動の創発」です。ハトやムクドリが大群となって飛んでいるところを見たことがある人も多いかと思います。鳥の大群は波のように動いたり一斉に向きを変えたりしますが、どうやって目的の方向に向かうのかというメカニズムはよくわかっていません。

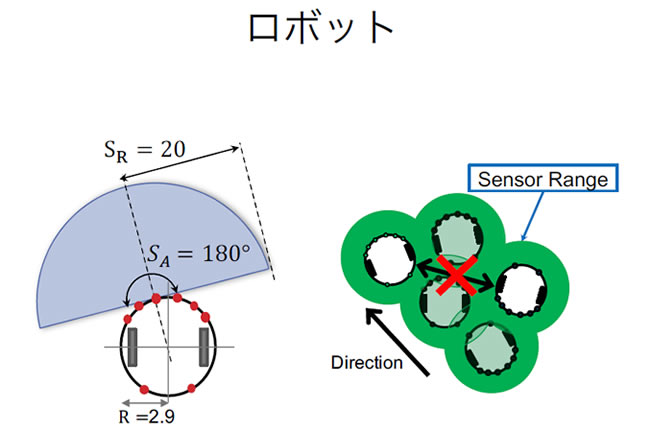
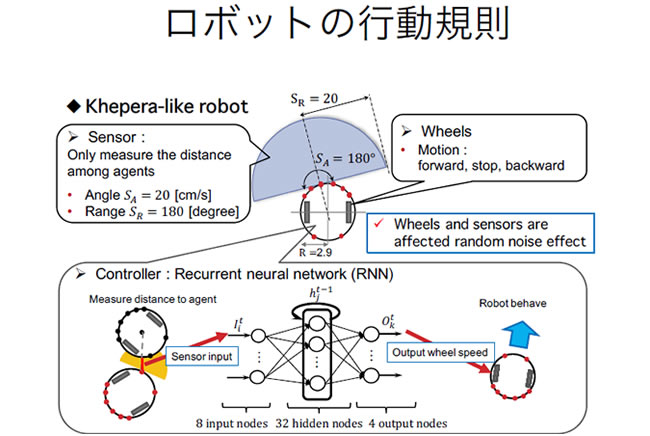
私たちは、お掃除ロボットのように二輪走行するロボットを用いて、お互いの運動しか認知できない状況下で、ロボット同士がどのようにコミュニケーションを取り、どのように行動を決定するかをシミュレーションしました。（解説１）。

3体のロボットにはセンサが搭載され、自分以外のロボットまでの距離が分かるようになっています。与えられたタスクは①お互い一定の範囲内の距離を保つこと、②できるだけ遠くまで移動することの２つだけです。3体のロボットは同じニューラルネットワークによって制御され、タスクを達成するために遺伝アルゴリズムによって進化していきます（動画１）。２〜３時間の進化のあと、最初はお互いの位置を探るように⼩刻みに動くのですが、そのコミュニケーションの中からどれか⼀体が先頭になり⼀列になって移動するようになります。つまり、コミュニケーションを通じて役割が生まれます。どのロボットが先頭になるかはランダムで、確率的には３分の一ずつです。現在は、学習した3体のロボットを10〜20体の群れの中に入れたらどうなるかという実験も進めています。

山本　⼆つめのテーマは人間の理解に関した研究テーマである「⾃⼰位置推定」です。 ロボットを自律的に動かすには自分の位置を正確に知らなければなりません。あらかじめマップが与えられていたり、対象物との距離が測れるセンサなどがあれば比較的簡単ですが、例えば災害が起きて建物の形が変わっていたり、GPSが使えない屋内などではロボットが自分で推定しなくてはなりません。

本研究で取り組んでいるのは、人間が周囲の景色を見て自分の位置を知るように、カメラを搭載したロボットが周囲の景色を撮影し、そこから自分の位置を推定するディープラーニング手法です（解説２）。

マインクラフトというゲーム環境の中に単眼カメラを搭載したロボットを置き、撮影しながら自分がどこにいるかを推定します。ロボットには、あらかじめ見えてる角度と地点を結びつけた座標をいくつか教えておきますが、移動後の画像との相違点を抽出し、そこから自分の位置を推定する方法はディープラーニングで学んでいきます。従来は「この景色が見えたらここ」という知識も教えなければなりませんでしたが、ディープラーニングでは正解の位置をいくつか教えておけば、場所が変わってもそこに結びつく特徴を自分で見つけだすことができます。しかし、ロボットが景色の中の何を特徴として捉えているかは私たちにはわかりません。そこがAIの特性なのです。

マインクラフトの環境での検証を行いました。移動ロボットに正解の座標をいくつか与えたのち、⾃分で撮影した数枚の写真を⼿がかりに⾃⼰位置推定します。検証の結果、最初の⼀枚では性能が落ちるのですが、2枚⽬以降では誤差が徐々に下がって、精度が上がっているのがわかりました。

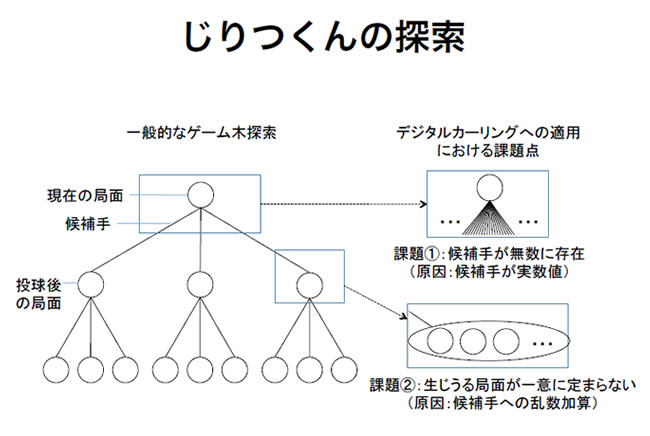
山本　三つめのテーマは「ゲームAIの開発」です。ゲームAIというと将棋やチェスなどが有名ですが、実はスポーツの世界でもゲームAIの技術が応用できます。その一つがカーリングです。最近人気のスポーツで「氷上のチェス」とも呼ばれています。なぜチェスなのかというと、ストーンを投げた後の配置（局面）から数手先を読みながらゲームを進めるからです。ただし、将棋やチェスは駒を置く場所（座標）が決まっていますが、カーリングは狙い通りの位置にストーンが行かないこともしばしばあります。そのため、先読みする場合の座標が確定していない（不確定要素が多い）のが大きな課題です。

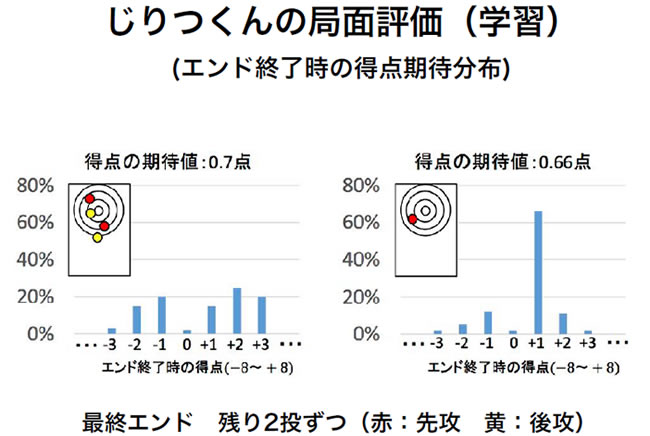
この課題を解決するため、私たちはデジタルカーリング（※）にボードゲームの検索手法を取り入れたAI「じりつくん」を開発しました（動画２）。じりつくんでは、Expectimaxによるゲーム木探索を行う手法を取り入れています（解説３）。狙い通りの場所にストーンが投げられなかった場合の可能性を確率分布によって吸収し、そこから先の試合展開と最終的な得点の期待値を計算して「どのぐらいの得点が得られるか」を計算します。

さらに、Expectimaxによるゲーム木探索によって得られたストーン座標値をニューラルネットワークに入れて機械学習させ、最終的に自分のチームが何点取る確率が高いかを計算させました（図２）。

実際のゲームでは、起こりうる局面が何通りもある上、プレイヤーの技量やアイスコンディションの影響で自分たちの望む座標にストーンを置けないという状況が発生します。私たちが開発したツールは、「このあたりを狙えば、多少のズレがあったとしても、最終的に得点が得られ、勝てる確率が高い」という予測をもたらすものです。プレイヤーだけでなくテレビ中継での解説などにも活用できると考えられ、実用化を目指して研究を続けているところです。

※電気通信⼤学の伊藤毅志研究室が中⼼となって開発したカーリング戦略⽀援ツール

(2017/11/28)